Grandezas inversamente proporcionais

Grandezas Inversamente Proporcionais: O Guia Definitivo para Descomplicar e Gabaritar

Você já se perguntou como algumas coisas no mundo parecem se comportar de maneira oposta? Quando uma aumenta, a outra diminui, mas não de qualquer jeito, e sim em uma relação perfeitamente proporcional?

O que são Grandezas e por que entendê-las é Crucial?

Antes de mergulharmos nas proporções, é fundamental entender o que é uma grandeza. Em termos simples, grandeza é tudo aquilo que pode ser medido ou contado. Pense em exemplos do seu dia a dia:

• Tempo (horas, minutos, segundos)

• Velocidade (km/h, m/s)

• Distância/Comprimento (km, metros, centímetros)

• Massa/Peso (kg, gramas)

• Volume (litros, m³)

• Quantidade de pessoas, objetos, etc.

• Preço

• Idade

• Temperatura

Por outro lado, coisas como "amor", "saudade" ou "imaginação" não são consideradas grandezas em matemática, pois não podem ser medidas ou contadas.

Entender as grandezas e como elas se relacionam é a base do raciocínio lógico. Isso facilita a interpretação de problemas, a montagem de equações e a resolução de questões não apenas em matemática, mas também em física e química. Sem essa compreensão, é fácil cair na armadilha da memorização de fórmulas, o que pode levar a confusões e erros em momentos cruciais.

Grandezas Diretamente Proporcionais: Uma Breve Revisão

Para que o conceito de grandeza inversamente proporcional seja ainda mais claro, vamos revisar rapidamente o que são as grandezas diretamente proporcionais.

Duas grandezas "x" e "y" são diretamente proporcionais (G.D.P.) quando, ao variar uma delas, a outra varia na mesma proporção [2, 10 (I), 17, 18, 20, 30, 40, 55]. Isso significa que:

• Se uma grandeza dobra, a outra também dobra.

• Se uma grandeza triplica, a outra também triplica.

• Se uma grandeza é dividida pela metade, a outra também é dividida pela metade.

A Representação Matemática de Grandezas Diretamente Proporcionais

Matematicamente, a relação entre duas grandezas diretamente proporcionais pode ser expressa de duas formas principais:

1. Como um quociente constante: Se "S" e "T" são grandezas diretamente proporcionais, então a divisão (quociente) entre elas é sempre um valor constante e positivo (k) [3, 4, 11 (c)]. Por exemplo, S/T = k.

2. Como uma equação linear: A forma mais comum é y = k ∙ x, onde x e y são as grandezas e k é a constante ou coeficiente de proporcionalidade.

Exemplo Prático: Imagine um carro se movendo em linha reta e uniforme a uma velocidade constante de 20 km/h.

• Em 1 hora, ele percorre 20 km.

• Em 2 horas, ele percorre 40 km.

• Em 3 horas, ele percorre 60 km.

• Em 4 horas, ele percorre 80 km.

Nesse caso, a relação matemática entre o espaço (S) e o tempo (T) é S = 20 ∙ T. Aqui, 20 é a constante de proporcionalidade (k). À medida que o tempo aumenta, o espaço percorrido aumenta na mesma proporção: se o tempo dobra, o espaço dobra.

O Gráfico das Grandezas Diretamente Proporcionais

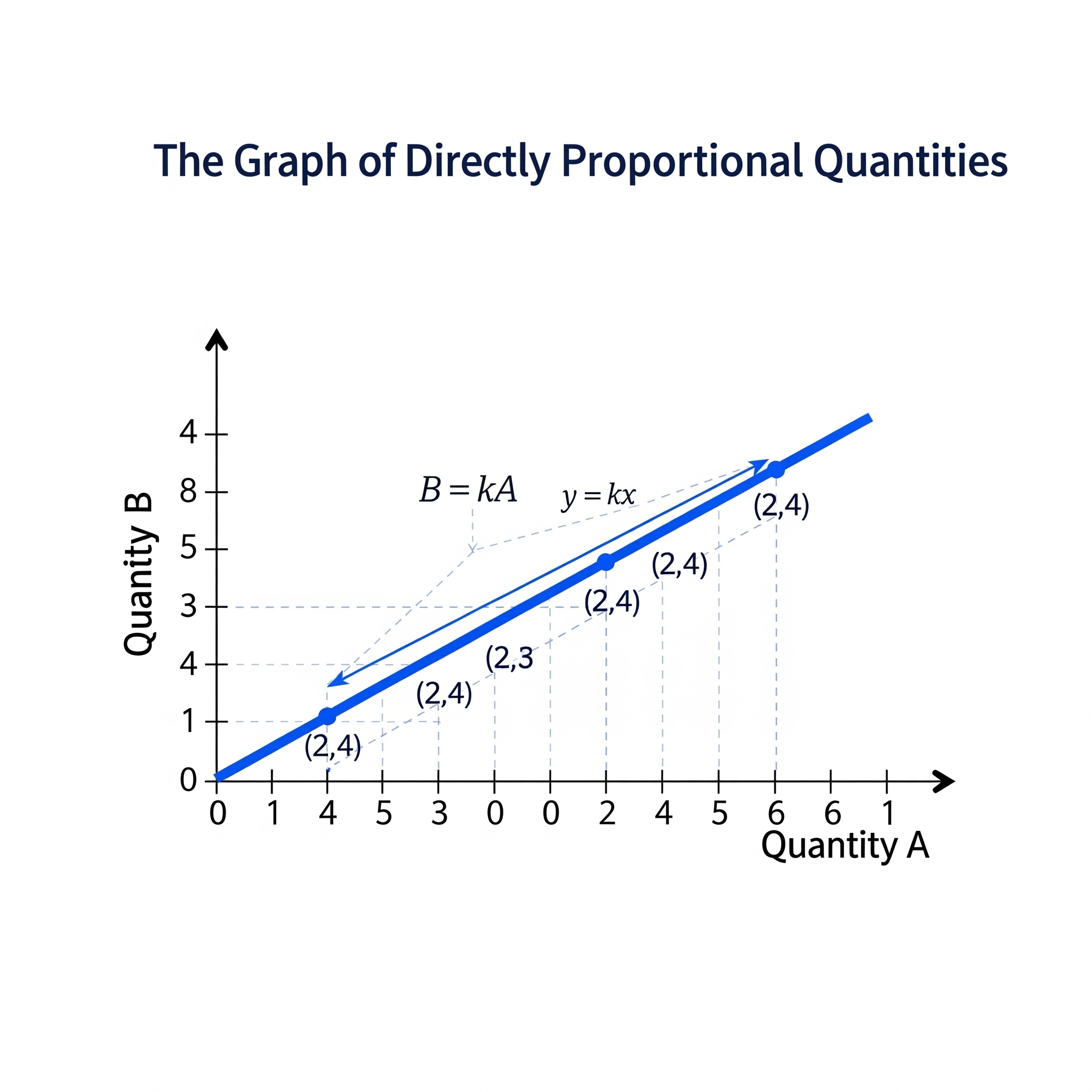
O gráfico que representa a relação entre duas grandezas diretamente proporcionais é sempre uma reta que parte da origem (0,0) e é crescente. Isso significa que, conforme um eixo (por exemplo, o tempo) avança, o outro eixo (o espaço) também avança de forma linear e proporcional.

Grandezas Inversamente Proporcionais: Desvendando o Conceito

Agora, a estrela do nosso guia: as grandezas inversamente proporcionais. Este é um conceito vital que aparece em muitos problemas complexos e que, uma vez dominado, simplifica muito o raciocínio.

Definição Clara e Objetiva

Duas grandezas "x" e "y" são chamadas de inversamente proporcionais (G.I.P.) quando um aumento na medida de uma delas faz com que a medida da outra seja reduzida na mesma proporção [5, 10 (III), 17, 18, 19, 20, 32, 41, 47, 55]. Em outras palavras:

• Se uma grandeza dobra, a outra é dividida por dois (reduzida pela metade).

• Se uma grandeza triplica, a outra é dividida por três (reduzida para um terço).

• Se uma grandeza é dividida pela metade, a outra dobra.

O ponto chave para identificar grandezas inversamente proporcionais é que o produto (a multiplicação) entre elas é sempre um valor constante e positivo.

A Fórmula da Relação Inversa

A relação matemática entre duas grandezas inversamente proporcionais pode ser representada por:

• y = k / x

• Ou, de forma equivalente, y ∙ x = k

Onde x e y são as grandezas, e k é a constante positiva de proporcionalidade. Essa constante representa o produto entre as duas grandezas em qualquer ponto da relação.

Exemplos Práticos do Dia a Dia

Para consolidar o entendimento, vejamos alguns exemplos clássicos de grandezas inversamente proporcionais:

1. Velocidade e Tempo para Percorrer uma Distância Fixa: Este é o exemplo mais comum e ilustrativo. Imagine que você precisa percorrer uma distância de 30 km.

   • Se sua velocidade é de 30 km/h, você levará 1 hora. (Produto: 30 km/h * 1h = 30 km)

   • Se sua velocidade é de 15 km/h (metade da anterior), você levará 2 horas (o dobro do tempo). (Produto: 15 km/h * 2h = 30 km)

   • Se sua velocidade é de 10 km/h (um terço da primeira), você levará 3 horas (o triplo do tempo). (Produto: 10 km/h * 3h = 30 km)

   • Se sua velocidade é de 60 km/h (o dobro da primeira), você levará 0,5 horas ou 30 minutos (metade do tempo). (Produto: 60 km/h * 0.5h = 30 km)

   Observe que, à medida que o tempo aumenta, a velocidade diminui na mesma proporção. O produto entre velocidade e tempo permanece constante em 30 km.

2. Número de Máquinas/Trabalhadores e Tempo para Concluir uma Tarefa: Se você dobrar o número de máquinas trabalhando ou o número de funcionários, o tempo necessário para realizar o mesmo serviço geralmente diminuirá pela metade [8 (b), 32]. Por exemplo, 20 funcionários produzem X barras de chocolate em 10 horas. Se o número de funcionários dobrar para 40, a mesma quantidade X de barras será produzida em 5 horas (metade do tempo).

3. Capacidade de Vasilhas e Número de Vasilhas para Encher um Tanque: Para encher um tanque, são necessárias 30 vasilhas de 6 litros cada. Se forem usadas vasilhas de 3 litros (metade da capacidade), serão necessárias 60 vasilhas (o dobro do número). A capacidade diminui, o número de vasilhas aumenta.

4. Resistência Elétrica e Área da Seção Transversal de um Fio Condutor: A resistência elétrica de um fio condutor é inversamente proporcional à área de sua seção transversal. Isso significa que quanto maior a "grossura do fio" (maior a área), menor será sua resistência em conduzir eletricidade.

Como Identificar Gráficos de Grandezas Inversamente Proporcionais

Uma das formas mais eficazes de identificar uma relação de proporcionalidade inversa é através da análise gráfica. O gráfico que representa duas grandezas inversamente proporcionais é sempre uma curva específica denominada hipérbole.

A hipérbole é caracterizada por uma curva que se aproxima dos eixos, mas nunca os toca. Ela mostra claramente que, enquanto uma grandeza aumenta (eixo x), a outra diminui (eixo y) de forma não linear, mas inversamente proporcional.

Importante: Evite a Pegadinha! Muitos estudantes confundem o gráfico de grandezas inversamente proporcionais com uma simples reta decrescente. Uma reta decrescente NÃO representa grandezas inversamente proporcionais. Uma reta decrescente indica que uma grandeza diminui quando a outra aumenta, mas não necessariamente na mesma proporção inversa exigida pela definição de proporcionalidade inversa. A hipérbole é a única representação gráfica correta para essa relação.

Regra de Três Simples para Grandezas Inversamente Proporcionais: O Passo a Passo

A regra de três é uma ferramenta poderosa e frequentemente cobrada em provas para resolver problemas que envolvem grandezas proporcionais, sejam elas diretas ou inversas. Para as grandezas inversamente proporcionais, há um passo crucial que não pode ser esquecido.

Para resolver situações usando a regra de três, siga estes passos fundamentais:

Os Três Passos Fundamentais

1. 1º Passo – Identificar as Grandezas e Montar a Tabela: Leia o problema com atenção e liste as grandezas envolvidas. Organize os valores conhecidos em uma tabela, colocando a grandeza desconhecida (x) no lugar apropriado.

2. 2º Passo – Analisar a Proporcionalidade: Este é o passo mais crítico. Determine se as grandezas são direta ou inversamente proporcionais. Pergunte-se: "Se uma grandeza aumenta, a outra aumenta (direta) ou diminui (inversa)?"

   • Se ambas aumentam ou ambas diminuem na mesma proporção: Diretamente Proporcionais.

   • Se uma aumenta e a outra diminui na mesma proporção: Inversamente Proporcionais.

3. 3º Passo – Aplicar o Método de Resolução Correto e Resolver a Equação:

   • Para Grandezas Diretamente Proporcionais: Multiplique os valores da tabela de forma cruzada.

   • Para Grandezas Inversamente Proporcionais: É necessário inverter uma das frações (trocar o numerador pelo denominador) antes de multiplicar cruzado. Este é o detalhe que muitos estudantes esquecem e que leva a erros!

Exemplo Detalhado com Regra de Três Inversa

Vamos usar um exemplo prático para ilustrar:

Problema: Para a confecção das provas de um concurso, uma gráfica dispunha de 15 impressoras, que demorariam 18 horas para imprimir todas as provas. No preparo para o início do trabalho, foi diagnosticado que só havia 10 impressoras funcionando. Qual é o tempo, em horas, que será gasto para a confecção de todas as provas do concurso?

Resolução:

1º Passo – Identificar as Grandezas e Montar a Tabela: As grandezas são: Quantidade de Impressoras e Tempo (em horas).

2º Passo – Analisar a Proporcionalidade: Se a quantidade de impressoras diminui (de 15 para 10), o tempo para fazer as impressões, consequentemente, aumentará. Logo, essas grandezas são inversamente proporcionais.

3º Passo – Aplicar o Método de Resolução Correto: Como são inversamente proporcionais, precisamos inverter uma das frações. Vamos inverter a primeira coluna (Impressoras):

Agora, multiplicamos cruzado: 10 * x = 15 * 18 10x = 270 x = 270 / 10 x = 27

Resposta: O tempo que será gasto para a confecção de todas as provas do concurso é de 27 horas.

Outro exemplo: Um automóvel desloca-se a 60 km/h e demora 3 horas para chegar ao seu destino. Se esse mesmo automóvel estivesse a 90 km/h, quanto tempo levaria para completar esse mesmo percurso?

Resolução: Grandezas: Velocidade (km/h) e Tempo (h).

Análise: Se a velocidade aumenta, o tempo diminui. São inversamente proporcionais. Invertendo uma fração (por exemplo, a da velocidade): 90 / 60 = 3 / x (ou seja, 90x = 3 * 60) 90x = 180 x = 180 / 90 x = 2

Resposta: Serão gastas duas horas a 90 km/h.

Dúvidas Comuns, Exceções e "Pegadinhas" em Provas

Esta seção é crucial para quem busca excelência, pois aborda as nuances e as armadilhas que frequentemente aparecem em questões de ENEM e concursos.

"Uma grandeza diminui, a outra aumenta, então é inversamente proporcional?"

Nem sempre! Este é um erro comum de raciocínio. Para que duas grandezas sejam inversamente proporcionais, a variação deve ocorrer na mesma proporção inversa. Ou seja, se uma dobra, a outra precisa ser dividida por dois; se uma triplica, a outra é dividida por três, e assim por diante.

Existe, por exemplo, a variação com o inverso do quadrado (f(x) = c / x²). Nesta relação, quando x aumenta, y diminui, mas não de forma diretamente inversa. Se x dobra, y é dividido por quatro, e não por dois. Apesar de y ser uma função decrescente de x, não se trata de uma relação de proporcionalidade inversa. Fique atento!

"Se X é inversamente proporcional a Y, então Y é diretamente proporcional a X?"

Falso! [10 (IV)] Esta é uma clássica "pegadinha" em provas teóricas. A definição de proporcionalidade (direta ou inversa) exige que a variação de uma grandeza reflita na outra na mesma proporção (seja ela direta ou inversa). Se X = k/Y, então Y = k/X. Ambas as relações são de proporcionalidade inversa. Não há uma transição automática para proporcionalidade direta.

Outra "pegadinha" teórica [10 (V)]: "Se duas grandezas X e Y são tais que ao aumentarmos o valor de X em n unidades, o valor de Y também aumenta em n unidades, então X e Y são grandezas diretamente proporcionais. Logo, para que duas grandezas sejam diretamente proporcionais elas sempre aumentam na mesma quantidade." Falso! A proporcionalidade direta não é sobre somar a mesma quantidade, mas sim sobre multiplicar pela mesma razão/fator [10 (V), 30]. Se X dobra, Y dobra; se X é dividido por 3, Y é dividido por 3. Não é uma relação aditiva, mas multiplicativa.

Proporcionalidade Mista: Quando as Coisas se Complicam

Em questões mais elaboradas de concursos, especialmente as que envolvem fórmulas da física, você pode encontrar situações onde uma grandeza é, ao mesmo tempo, diretamente proporcional a uma ou mais grandezas e inversamente proporcional a outras.

A fonte apresenta uma relação geral: A ∙ B / C = k (onde k > 0). Analisando essa expressão, podemos inferir:

• A e B são inversamente proporcionais, se C for constante (pois A ∙ B = k ∙ C, e k ∙ C seria uma nova constante).

• A e C são diretamente proporcionais, se B for constante (pois A / C = k / B, e k / B seria uma nova constante).

• Neste caso, a grandeza A é diretamente proporcional a C e inversamente proporcional a B.

Exemplo do Hércules (Questão 06): Hércules disse que sua força ('H') é:

• Diretamente proporcional ao quadrado da força do Leão da Nemeia (L²).

• Diretamente proporcional à rapidez da Hidra de Lerna (R).

• Inversamente proporcional ao medo das amazonas (M).

Sendo k uma constante de proporcionalidade, a expressão que representa a força de Hércules é: H = k ∙ (L² ∙ R) / M [14 (C) - corrigida para forma padrão]

Essa relação pode ser reescrita como: H ∙ M / (L² ∙ R) = k. Isso demonstra claramente como diferentes tipos de proporcionalidade podem coexistir em uma única expressão, exigindo uma análise cuidadosa de cada relação.

Preparação para ENEM e Concursos Públicos: Dominando as Grandezas Proporcionais

O tema de grandezas proporcionais, tanto diretas quanto inversas, é extremamente recorrente em exames como o ENEM e em provas de concursos públicos. A razão é simples: ele testa seu raciocínio lógico e sua capacidade de aplicar conceitos matemáticos a situações-problema do cotidiano.

Por que esse tópico é tão cobrado?

• Aplicação Prática: Muitos problemas da vida real envolvem proporcionalidade, como cálculos de velocidade, rendimento de trabalho, consumo de combustível, dosagens de medicamentos, etc.

• Raciocínio Lógico: As questões exigem que você identifique a relação entre as grandezas, e não apenas que aplique uma fórmula decorada. Isso impede que o aluno simplesmente memorize e o força a pensar.

• Base para Outros Conteúdos: Proporcionalidade é a base para tópicos mais avançados em matemática (como funções lineares e inversas) e física (cinemática, dinâmica, eletricidade).

Tipos de Questões Comuns:

1. Identificação de Proporcionalidade: São questões teóricas ou com pequenos exemplos que pedem para você classificar a relação entre duas grandezas como direta (D), inversa (I) ou não proporcional.

   • Exemplo: "O número de máquinas trabalhando e o tempo que levam para construir um foguete." (Resposta: Inversamente Proporcional) [8 (b)].

   • Exemplo: "A velocidade de um ônibus e a distância percorrida por ele em três horas." (Resposta: Diretamente Proporcional, pois em tempo constante, maior velocidade implica maior distância) [8 (d)].

2. Análise de Gráficos: Você precisará identificar se um gráfico representa uma relação diretamente proporcional (reta crescente da origem) ou inversamente proporcional (curva tipo hipérbole).

   • Lembre-se: hipérbole para inversa, reta da origem para direta.

3. Problemas com Regra de Três (Simples e Composta): A grande maioria das questões de cálculo. Você precisará aplicar os três passos: identificar grandezas, analisar a proporcionalidade e resolver a equação (lembrando-se de inverter a fração em casos inversos!). O ENEM adora problemas de regra de três, muitas vezes disfarçados em contextos cotidianos.

   • A regra de três simples envolve apenas duas grandezas.

   • A regra de três composta envolve três ou mais grandezas, e pode misturar relações diretas e inversas no mesmo problema. É uma extensão da regra de três simples e requer mais atenção na análise de cada par de grandezas em relação àquela que contém o x.

4. Questões de Julgamento (Certo/Errado ou Verdadeiro/Falso): Testam seu conhecimento conceitual, abordando as definições e as "pegadinhas" que discutimos.

   • Exemplo: "Dadas duas grandezas inversamente proporcionais, quando uma delas diminui a outra também diminui na mesma proporção." (Resposta: FALSO, pois a outra AUMENTA na mesma proporção) [9 (IV)].

Dicas Finais para o Sucesso:

• Pratique Constantemente: A familiaridade com os diferentes cenários e a agilidade na identificação da proporcionalidade vêm com a prática. Faça muitos exercícios de grandezas proporcionais.

• Desenhe a Tabela: Mesmo para problemas simples, montar a tabela ajuda a visualizar as grandezas e seus valores, evitando erros.

• Analise Antes de Calcular: Nunca comece a calcular antes de ter certeza se a relação é direta ou inversa. O passo de análise é o mais importante para não errar a montagem da equação.

• Compreenda, Não Decore: A física e a matemática são muito mais fáceis quando você entende a lógica por trás das fórmulas. As fórmulas são um resumo da teoria. Entender a proporção entre grandezas vai te ajudar a "não esquecer a fórmula e não confundir onde uma grandeza deve estar (em cima/baixo, numerador/denominador)".

Continue estudando e exercitando! O sucesso está ao seu alcance!